Je hebt tandpijn. Je blaast een rode ballon op, en de pijn verdwijnt. Is dit toeval, of helpen rode ballonnen tegen tandpijn? Gezondheid en Wetenschap legt uit hoe statistiek kan helpen bij het definiëren van toeval.
Wat is toeval?
Een interventiestudie met 2 deelnemersgroepen onderzoekt een eetlustremmer. De deelnemers in de interventiegroep krijgen een eetlustremmer, met als resultaat een daling van het gewicht bij 12 personen op 50. De deelnemers in de controlegroep krijgen een placebo (controlemiddel), met gewichtsverlies bij slechts 3 personen op 50 als resultaat.
Een woordje uitleg …
In een ideale wereld met ideale studies zouden we geen statistiek nodig hebben, tot grote vreugde van vele studenten.
Voorbeeld 1
Als voorbeeld nemen we een interventiestudie die een eetlustremmer test. Figuur 1 geeft 2 groepen deelnemers met overgewicht weer: 50 deelnemers krijgen een eetlustremmer en 50 deelnemers een controlemiddel.
Figuur 1
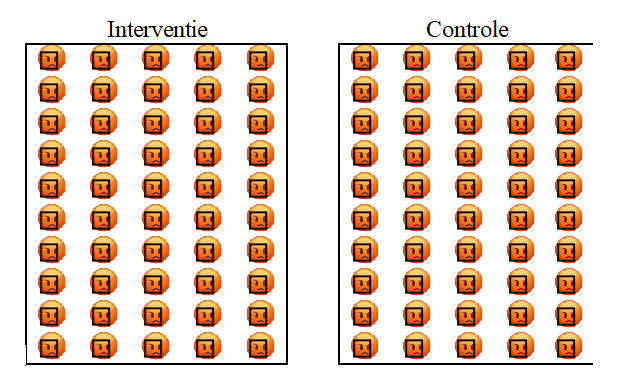
Figuur 2 geeft de ideale wereld weer na een bepaalde periode: alle deelnemers uit de interventiegroep zijn gelukkig, omdat ze gewicht verloren. Dit was niet het geval in de controlegroep, waar niemand gewicht verloor.
Figuur 2
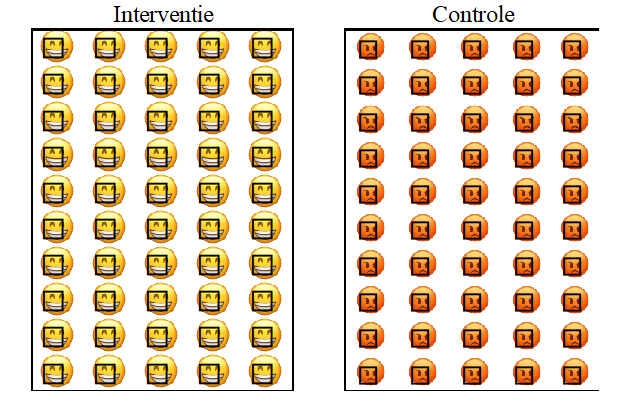
Conclusie van de studie: onze eetlustremmer is een succes, want iedereen vermagert. Kassa, kassa, we kunnen het product verkopen!
De werkelijkheid is echter veel ingewikkelder, omdat personen in de interventiegroep vaak geen resultaat laten zien, en mensen in de controlegroep wel. In ons voorbeeld betekent dit dat mensen in de interventiegroep geen gewicht verliezen ondanks de eetlustremmer, en mensen uit de controlegroep wel vermageren zonder eetlustremmer.
- Hoe kunnen we dan weten of de eetlustremmer werkt of niet? We moeten dus het verschil kunnen maken tussen een echte vondst en toeval: hiervoor is statistiek essentieel.
Voorbeeld 2
Een tweede voorbeeld: we vertrekken met dezelfde mensen uit figuur 1. De situatie op het einde van de interventiestudie is figuur 3 (zie onder). In de interventiegroep verliezen 12 mensen van de 50 gewicht, en in de controlegroep 6 van de 50.
- De vraag is nu: werkt de eetlustremmer en mogen we dit product verkopen, of is het verschil enkel te wijten aan toeval?
- Als toeval een grote rol speelt, dan kunnen we de verkoop van de eetlustremmer vergeten, aangezien een nepmiddel (controlemiddel) even goed blijkt te werken.
Figuur 3
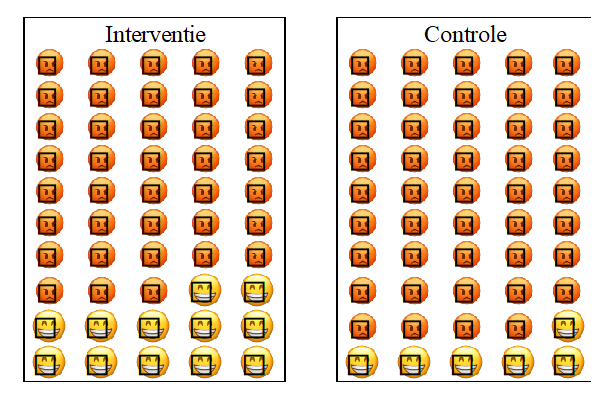
Om deze vraag te beantwoorden, geeft de statistiek eerst het toeval een definitie. Als de waarschijnlijkheid dat iets gebeurt 5% of minder is, dan kunnen we stellen dat toeval een kleine rol speelt. Het idee hierachter is eenvoudig: laten we aannemen dat een rode kaart betekent dat de eetlustremmer niet werkt, en een groene kaart dat de eetlustremmer wel werkt.
Als er 100 kaarten voor je liggen, met 50 rode en 50 groene, dan is de kans op rood 50%. Liggen er 30 rode en 70 groene, dan is de kans op rood lager, namelijk 30%. In de statistiek zeggen we: als er 5 rode kaarten liggen en 95 groene, dan is de kans op rood vrij laag, namelijk 5%. We kunnen er dan bijna zeker van zijn dat de kans op rood (= de eetlustremmer werkt niet) zeer laag is. Volledige zekerheid heb je natuurlijk pas als er 100 groene kaarten liggen (= de eetlustremmer werkt wel), maar dat is de ideale wereld.
Het toeval berekenen met de p-waarde
Omdat we nooit echt zeker zijn van iets, en niets meer zouden beslissen als we op zekerheid zouden wachten, proberen we het toeval te definiëren. In de statistiek drukken we dit uit met de p-waarde (‘p’ van probability of waarschijnlijkheid). Een p-waarde gelijk aan of kleiner dan 0,05 betekent dat het toeval 5% of minder bedraagt. Het berekenen van de p-waarde gebeurt met verschillende statistische testen: naargelang de gegevens moet je de juiste test gebruiken, wat soms niet eenvoudig is. In het geval van de eetlustremmer-studie willen we de deelnemers die gewicht verliezen door de interventie (de eetlustremmer) onderscheiden van de deelnemers die toevallig vermageren.
Voor figuur 3 is p=0,12, dus groter dan 0,05, want 12% is meer dan 5%. Er zijn dus 12 rode kaarten en 88 groene, wat de kans op rood toch vrij groot maakt. Conclusie: je kunt niet zomaar besluiten dat de toegediende eetlustremmer werkt.
Waren er nu 12 personen in de interventiegroep en 3 in de controlegroep, dan was p=0,01! Anders gezegd: als er slechts 1 rode kaart op 100 is, is de kans om deze te trekken klein. In dat geval mogen we de eetlustremmer verkopen.
Conclusie
Om uit te maken of studieresultaten te wijten zijn aan een bepaalde interventie, dan wel aan puur toeval, kan statistiek ons helpen. Met de zogenaamde 'p-waarde' kunnen we toeval een definitie geven. Dat tandpijn zou verdwijnen door een rode ballon op te blazen, is waarschijnlijk toch eerder een kwestie van toeval dan een effectieve behandeling.

